Uma das vantagens do índice invertido é a possibilidade de otimizar os algoritmos utilizados nas consultas. Esses algoritmos já são implementados por set no python, mas não garantem a sequência dos ids dos documentos e também não permitem algumas otimizações. Portanto, é necessário passar por esses algoritmos para ver as extensões e como elas podem ajudar.

intersecção de conjuntos Link para o cabeçalho

Uma consulta casa AND blumenau precisa efetuar a intersecção entre os documentos de casa e os documentos de blumenau. O algoritmo de intersecção é uma solução para esse problema

# Introduction to Information Retrieval, p. 11

def intersect(p1, p2):
    answer = []
    p1_i = 0
    p2_i = 0
    while len(p1) > p1_i and len(p2) > p2_i:
        if p1[p1_i] == p2[p2_i]:
            answer.append(p1[p1_i])
            p1_i += 1
            p2_i += 1
        elif p1[p1_i] < p2[p2_i]:
            p1_i += 1
        else:
            p2_i += 1
    return answer


assert intersect([1, 2, 3], [2, 4]) == [2]
assert intersect([5, 6], [5, 6]) == [5, 6]
assert intersect([1], [2, 4]) == []
assert intersect([7], [2, 4]) == []
assert intersect([], []) == []

O algoritmo é um tanto quanto simples:

  • Recebe como entrada duas listas com ids de documentos
  • Se os ids são iguais p1[p1_i] == p2[p2_i]
    • Adiciona no resultado
    • Move os índices das duas listas
  • Se o id de p1 é menor que p2
    • Move o índice de p1
    • Nesse caso p1[p1_i] já foi adicionado, ou não existe em p2
  • Senão
    • Move o índice de p2
    • Nesse caso p2[p2_i] já foi adicionado, ou não existe em p1
  • Retorna a lista com os documentos que ocorrem em p1 e p2
    • É possível notar que a lista também está ordenada

união de conjuntos Link para o cabeçalho

Seguindo a mesma ideia é possível, efetuar as operações union (união de conjuntos) e diff (diferença de conjuntos).

def union(p1, p2):
    answer = []
    p1_i = 0
    p2_i = 0
    while len(p1) > p1_i or len(p2) > p2_i:
        if p1_i == len(p1):
            answer.append(p2[p2_i])
            p2_i += 1
        elif len(p2) == p2_i:
            answer.append(p1[p1_i])
            p1_i += 1
        elif p1[p1_i] == p2[p2_i]:
            answer.append(p1[p1_i])
            p1_i += 1
            p2_i += 1
        elif p1[p1_i] < p2[p2_i]:
            answer.append(p1[p1_i])
            p1_i += 1
        else:
            answer.append(p2[p2_i])
            p2_i += 1
    return answer


assert union([1, 2, 3], [2, 4]) == [1, 2, 3, 4]
assert union([5, 6], [5, 6]) == [5, 6]
assert union([1], [2, 4]) == [1, 2, 4]
assert union([7], [2, 4]) == [2, 4, 7]
assert union([], []) == []

Note que esse algoritmo pode não ser a melhor implementação, visto que não tem referência no livro. Mesmo assim, a ideia é:

  • Recebe como entrada duas listas com ids de documentos
  • Se p1 terminou, mas ainda tem documentos em p2
    • Adiciona no resultado
    • Move o índice de p2
  • Se p2 terminou, mas ainda tem documentos em p1
    • Adiciona no resultado
    • Move o índice de p1
  • Se os documentos são iguais
    • Adiciona no resultado
    • Move os índices de p1 e p2
  • Se o id de p1 é menor que p2
    • Adiciona no resultado
    • Move o índice de p1
    • Nesse caso p1[p1_i] já foi adicionado, ou não existe em p2
  • Senão
    • Adiciona no resultado
    • Move o índice de p2
    • Nesse caso p2[p2_i] já foi adicionado, ou não existe em p1
  • Retorna a lista com os documentos que ocorrem em p1 e p2
    • É possível notar que a lista também está ordenada

diferença de conjuntos Link para o cabeçalho

def diff(p1, p2):
    answer = []
    p1_i = 0
    p2_i = 0
    while len(p1) > p1_i:
        if len(p2) == p2_i or p1[p1_i] < p2[p2_i]:
            answer.append(p1[p1_i])
            p1_i += 1
        elif p1[p1_i] == p2[p2_i]:
            p1_i += 1
            p2_i += 1
        else:
            p2_i += 1
    return answer


assert diff([1, 2, 3], [2, 4]) == [1, 3]
assert diff([5, 6], [5, 6]) == []
assert diff([1], [2, 4]) == [1]
assert diff([7], [2, 4]) == [7]
assert diff([], []) == []

Mesma ideia que union, pode não ser a melhor implementação.

  • Recebe como entrada duas listas com ids de documentos
  • Se p2 terminou ou o id de p1 é menor que p2
    • Adiciona no resultado
    • Move o índice de p1
  • Se os documentos são iguais
    • Move os índices de p1 e p2
  • Senão
    • Move o índice de p2
    • Nesse caso p2[p2_i] não existe em p1
  • Retorna a lista com os documentos que ocorrem em p1 e p2
    • É possível notar que a lista também está ordenada

A partir dessas implementações é possível reescrever consultas com AND, OR NOT.

print('voters AND jury')
voters = inverted_index['voters']
jury = inverted_index['jury']
doc_ids = intersect(voters, jury)
for doc_id in doc_ids:
    print('> ', ' '.join(DOCUMENTOS[doc_id]))
    
print('voters OR jury')
voters = inverted_index['voters']
jury = inverted_index['jury']
doc_ids = union(voters, jury)
for doc_id in doc_ids:
    print('> ', ' '.join(DOCUMENTOS[doc_id]))

print('voters AND NOT city')
voters = inverted_index['voters']
city = inverted_index['city']
not_city = diff(inverted_index['__alldocs__'], city)
doc_ids = intersect(voters, not_city)
for doc_id in doc_ids:
    print('> ', ' '.join(DOCUMENTOS[doc_id]))

otimização de consultas AND Link para o cabeçalho

Entretanto, até o momento esses algoritmos são simples implementações sem nenhum tipo de otimização. A primeira otimização, também poderia ser feita usando set, é que, em consultas AND, se executar primeiro as listas com menos documentos a execução fica mais rápida. O motivo é que, no final, são feitas menos comparações, porque listas maiores ficaram para o fim. Assim, é possível executar uma combinação de consultas AND ordenando pelo quantidade de documentos. Note que isso só é válido para AND (intersecção) e porque AND é comutativo, portanto, casa AND blumenau é o mesmo que blumenau AND casa.

# Introduction to Information Retrieval, p. 12

def conjunctive_intersect(*p):
    postings = sorted(p, key=lambda x: len(x))
    result = postings[0]
    postings = postings[1:]
    while postings and result:
        result = intersect(result, postings[0])
        postings = postings[1:]
    return result


assert conjunctive_intersect([1, 2, 3], [2, 4]) == [2]
assert conjunctive_intersect([5, 6], [5, 6]) == [5, 6]
assert conjunctive_intersect([1], [2, 4]) == []
assert conjunctive_intersect([7], [2, 4]) == []
assert conjunctive_intersect([], []) == []

assert conjunctive_intersect([1, 2, 3], [2, 4], [1, 2, 4]) == [2]
assert conjunctive_intersect([5, 6], [5, 6], [5, 6]) == [5, 6]
assert conjunctive_intersect([1], [2, 4], [1]) == []
assert conjunctive_intersect([7], [2, 4], [5], [1]) == []
assert conjunctive_intersect([], [], [1]) == []
assert conjunctive_intersect([], [], [], []) == []

Essa implementação usa intersect definido anteriormente, mas antes faz uma ordenação pela quantidade de documentos. Um detalhe é que consultas casa AND (blumenau OR gaspar) AND venda também podem ser otimizadas. O motivo é que é possível fazer uma estimativa do tamanho de (blumenau OR gaspar) apenas somando a quantidade de documentos em cada lista. Assim, qualquer consulta com AND pode ser otimizada, independente de ser composta ou não.

consultas com skip list Link para o cabeçalho

Ainda assim, nenhuma otimização que justifique a troca de set pelas implementações de intersect, union e diff. Outra otimização que pode ser feita é o uso de uma skip list. Uma skip list é uma estrutura de dados, estilo uma lista encadeada, mas alguns nós possuem um ponteiro para elementos mais a frente na lista, além do próximo elemento. Dessa forma, ao percorrer os elementos da lista é possível verificar elementos mais a frente à fim de saber se é possível pular comparações ou se é necessário passar elemento por elemento.

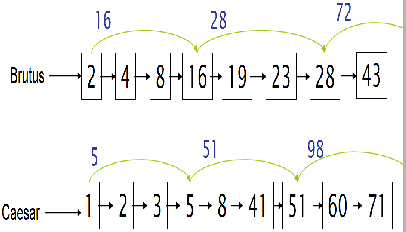Exemplo de uma skip list. Fonte: Introduction to Information Retrieval

No exemplo acima, o termo Brutus possui os skip pointers:

  • 16 na posição 0
  • 28 na posição 3
  • 72 na posição 6
  • Assim por diante

A detalhe é onde colocar os skip pointers. Uma sugestão é colocar a cada $\sqrt{N}$ elementos em uma lista com $N$ elementos. Agora é necessário implementar uma versão de skip list para melhorar o tempo de busca.

from math import sqrt


class SkipList(list):
    
    def skip(self, i):
        p = len(self)
        skip_size = int(sqrt(p))
        if skip_size and i < p - 1 and i % skip_size == 0:
            return min(i + skip_size, p - 1)
        return None


sl = SkipList()
assert sl.skip(0) is None

sl = SkipList([1])
assert sl.skip(0) is None

sl = SkipList([1, 2])
assert sl.skip(0) == 1
assert sl.skip(1) is None

sl = SkipList([1, 2, 3])
assert sl.skip(0) == 1
assert sl.skip(1) == 2
assert sl.skip(2) is None

sl = SkipList([1, 2, 3, 4])
assert sl.skip(0) == 2
assert sl.skip(1) is None
assert sl.skip(2) == 3
assert sl.skip(3) is None

sl = SkipList([1, 2, 3, 4, 5, 6, 7, 8, 9])
assert sl.skip(0) == 3
assert sl.skip(1) is None
assert sl.skip(2) is None
assert sl.skip(3) == 6
assert sl.skip(4) is None
assert sl.skip(5) is None
assert sl.skip(6) == 8
assert sl.skip(7) is None
assert sl.skip(8) is None

sl = SkipList([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
assert sl.skip(0) == 3
assert sl.skip(1) is None
assert sl.skip(2) is None
assert sl.skip(3) == 6
assert sl.skip(4) is None
assert sl.skip(5) is None
assert sl.skip(6) == 9
assert sl.skip(7) is None
assert sl.skip(8) is None
assert sl.skip(9) is None

Note que a implementação estende list do python para manter o mesmo comportamento de lista. O detalhe é a adição do método skip que calcula o próximo índice a ser buscado, caso deseje tentar pular comparações. Obviamente não é a melhor implementação de uma skip list, mas é o suficiente para testar a intersecção com essa estrutura.

# Introduction to Information Retrieval, p. 37

def intersect_with_skips(p1, p2):
    p1 = SkipList(p1)
    p2 = SkipList(p2)
    answer = []
    p1_i = 0
    p2_i = 0
    while len(p1) > p1_i and len(p2) > p2_i:
        if p1[p1_i] == p2[p2_i]:
            answer.append(p1[p1_i])
            p1_i += 1
            p2_i += 1
        elif p1[p1_i] < p2[p2_i]:
            if p1.skip(p1_i) and p1[p1.skip(p1_i)] <= p2[p2_i]:
                while p1.skip(p1_i) and p1[p1.skip(p1_i)] <= p2[p2_i]:
                    p1_i = p1.skip(p1_i)
            else:
                p1_i += 1
        else:
            if p2.skip(p2_i) and p2[p2.skip(p2_i)] <= p1[p1_i]:
                while p2.skip(p2_i) and p2[p2.skip(p2_i)] <= p1[p1_i]:
                    p2_i = p2.skip(p2_i)
            else:
                p2_i += 1

    return answer


assert intersect_with_skips([1, 2, 3], [2, 4]) == [2]
assert intersect_with_skips([5, 6], [5, 6]) == [5, 6]
assert intersect_with_skips([1], [2, 4]) == []
assert intersect_with_skips([7], [2, 4]) == []
assert intersect_with_skips([], []) == []

assert intersect_with_skips(
    [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    [2, 4]
) == [2, 4]
assert intersect_with_skips(
    [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    [8, 9, 10, 11, 12, 13]
) == [8, 9, 10]

Note que o algoritmo segue a mesma ideia de intersect, mas faz o uso da skip list quando p1[p1_i] < p2[p2_i] ou p2[p2_i] < p1[p1_i]. Nesse caso, a busca tenta evitar comparações pegando o id em p1.skip(p1_i) e comparando com o id atual de p2. Se for menor, é possível pular até p1.skip(p1_i) e fazer a mesma verificação. Se não for, continua a execução normal da intersecção.

Finalmente, é bem provável que seja possível trocar a skip list por algo similar à busca binária, visto que os ids estão sempre ordenados. Talvez seja uma alternativa para não precisar calcular/manter os skip pointers.

Referências: Link para o cabeçalho