Olá, tudo certo!?
Hoje vamos trabalhar com a ideia de desenhar o símbolo do Batman com equações. Veremos alguns conceitos matemáticos que permitem fazer esse desenho. O desenho que eu vou demonstrar é um que fiz e talvez não seja com as melhores fórmulas nem a forma otimizada, mas acho que ele é bom um passo a passo sobre alguns conceitos da álgebra. O desenho é composto por retas, parábolas e círculos. A partir destes componentes básicos, aplicamos transformações e restrições no domínio da equação que formam o desenho. Para fazer o desenho vamos usar o Desmos (calculadora gráfica online).
Ao infinito e além: desenhando a cabeça do morcego com retas
Vamos começar pelos componentes mais simples que são as retas. Usamos três retas para desenhar a cabeça e as orelhas do morcego como pode ser visto da Figura 1.
Figura 1 - Retas que formam a cabeça do morceço
Os valores entre {} limitam os valores (domínio) de x na equação. Por exemplo, a equação só terá valores para y quando x estiver entre -0.5 e 0.5.
As duas retas inclinadas seguem uma intuição semelhante, mas tem equações diferentes. A reta da direita (laranja) pode ser desenhada com a equação $y = 2x + 5 {0.5 < x < 1} $ e a reta da esquerda com $ y = -2x + 5 {-1 < x < -0.5} $. É possível perceber que as equações são muito parecidas e agora vamos ver porque as retas podem ser desenhadas com as equações anteriores.
Por que as retas se comportam dessa forma?
Existem três retas (que eu conheço) que são super simples $ x = 1 $ (reta roxa na Figura 2), $ y = 1 $ (reta laranja na Figura 2) e $ y = x $ (reta preta na Figura 2). A reta $ x = 1 $ é uma reta vertical que passa por qualquer coordenada no eixo y, mas apenas na coordenada 1 no eixo x. A reta $ y = 1 $ é uma reta horizontal que passa em qualquer coordenada no eixo x, mas apenas na coordenada 1 do eixo y. A reta $ y = x $ é uma diagonal que passa em qualquer coordenada no eixo x e também em qualquer coordenada do eixo y.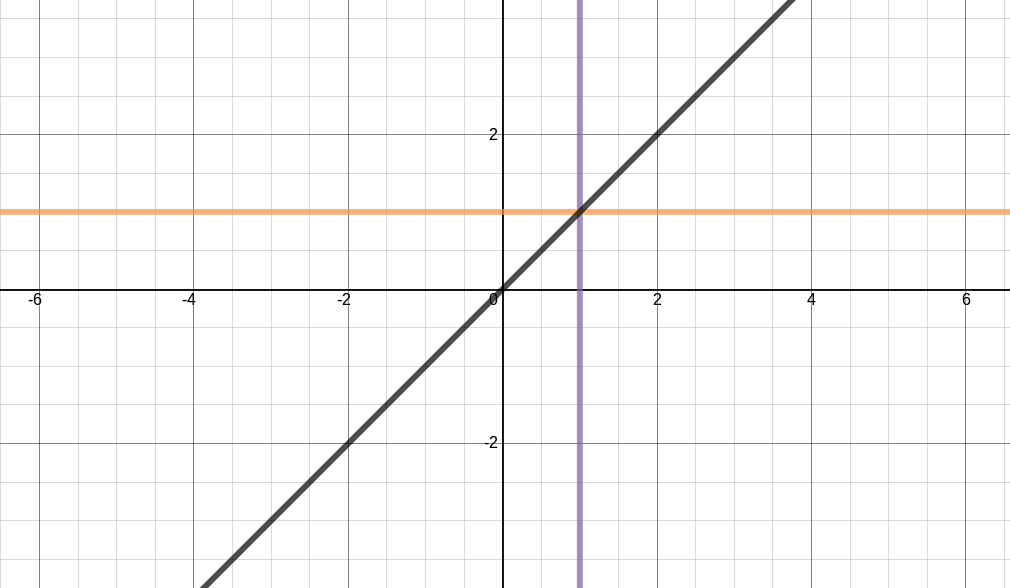
Figura 2 - Exemplos de retas vertical, horizontal e diagonal.
As equações anteriores podem ser alteradas com transformações que mudam o comportamento da reta. Alterando $ y = x $ para $ y = x + 2 $ é possível perceber que a reta foi deslocada um pouco para cima, passando pelo eixo y no ponto (0, 2). Agora se alterar a reta para $ y = x - 5 $ é possível perceber que a reta foi deslocada um pouco para baixo passando pelo eixo y no ponto (0,-5). Isso demonstra que é possível construir uma reta apenas sabendo em qual coordenada ela passa pelo eixo y.
Pergunta: Como construir uma reta que passe no eixo y no ponto (0, 7)? Resposta: A equação para essa reta é $ y = x + 7 $.
As equações estão no formato $ y = mx + b $ sendo:
- b a coordenada y que corta o eixo y;
- m é a inclinação da reta.
Até mesmo a reta $ y = 1 $ está nesse formato, mas no caso dela $ y = 0x + 1 $ por isso $ y = 1 $ o 0x é porque ela não tem inclinação. A reta $ y = x $ também está neste formato, mas com a coordenada y com valor 0 porque ela passa pela origem.
A inclinação da reta é o quanto a reta muda em y em relação ao quanto a reta muda em x. Nas retas acima, exceto $ y = 1 $, é possível perceber que a reta tem inclinação 1. A inclinação 1 indica uma variação de 1 para 1 entre x e y, ou seja, ela move 1 em x e 1 em y. Como é possível descobrir a inclinação? Simples, mas é necessário saber 2 pontos onde reta passa e a equação $ m = \frac{y_2 - y_1}{x_2 - x_1} $. Utilizando os pontos (-7, 0) e (-6, 1) da reta $ y = x + 7 $ e aplicando-os na equação obtém-se $ m = \frac{1 - 0}{-6 - (-7)} = \frac{1}{-6 + 1} = \frac{1}{1} = 1 $ validando a inclinação (m) da equação $ y = x + 7 $.
Questão: Qual a equação de uma reta que tem $ m = \frac{2}{3} $ e passa no eixo y no ponto (0, -9)?
Resposta: A equação é $ y = \frac{2}{3}x + 3 $.
Questão: Qual a equação de uma reta que passa pelos pontos (0, 3) e (3, 13)?
Resposta: A inclinação é $ m = \frac{3 - 13}{0 - 3} = \frac{-10}{-3} = \frac{10}{3} $ e a reta é $ y = \frac{10}{3}x - 9 $.
Obtendo o sinal de parabólica: desenhando as asas com parábolas
As asas do morcego são desenhadas com seis parábolas. São duas parábolas para a parte superior e duas para a parte inferior demonstradas na Figura 3.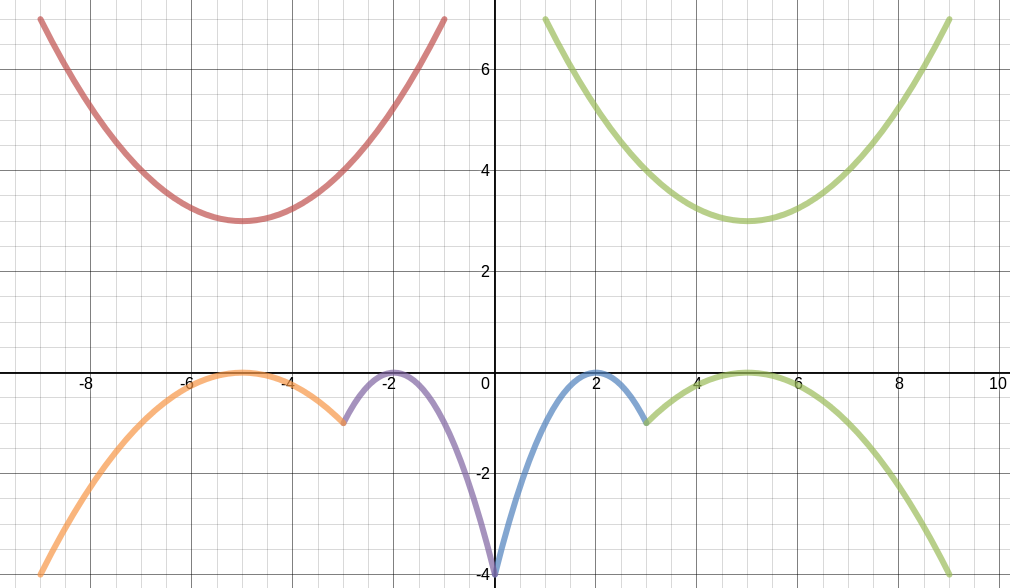
Figura 3 - Parábolas que formam as asas do morcego.
Por que as parábolas se comportam dessa forma?
A parábola mais simples é $ y = x^2 $ (parábola vermelha na Figura 4) e as demais parábolas são criadas aplicando transformações nessa parábola. As parábolas possuem (da mesma forma que as retas) uma intercepção em y (ponto que passa pelo eixo y). Também é possível notar uma intercepção em x (ponto que passa pelo eixo x). As parábolas podem ter 1, 2 ou nenhuma intercepção em x como nos exemplos a seguir:
- $ y = x^2 + 2 $ (parábola verde na Figura 4) não possui intercepção em x (não passa nenhuma vez pelo eixo x).
- $ y = x^2 - 2 $ (parábola azul na Figura 4) possui duas intercepções em x (passa duas vezes pelo eixo x).
As transformações acima são semelhantes as aplicadas na reta, adicionando um termo sem variável na equação move o resultado no eixo y.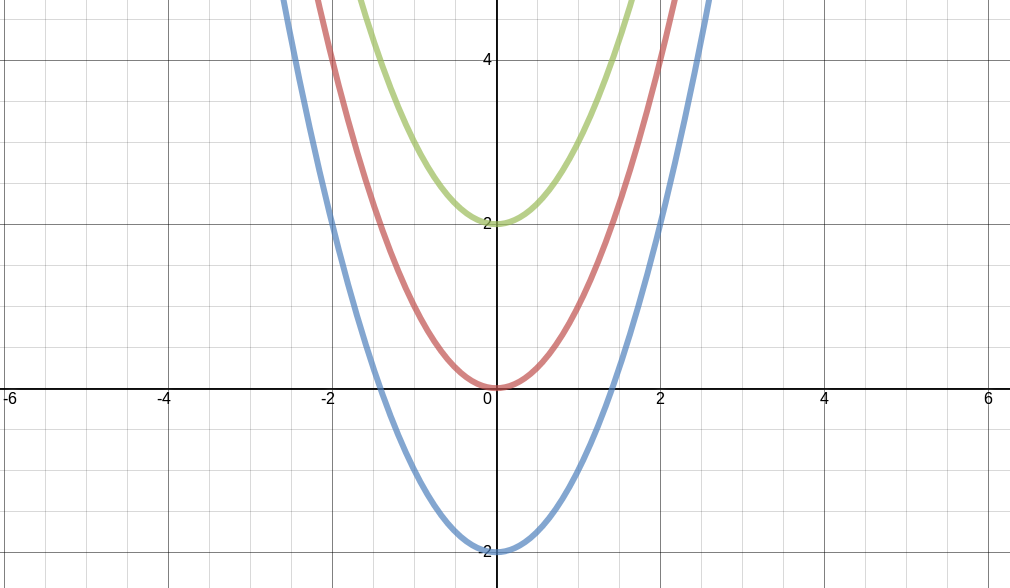
Figura 4 - Exemplos de transformações em parábolas no eixo y.
As parábolas também podem ser movimentadas na horizontal pelo eixo x e para isso é necessário alterar o termo $ x^2 $. Para mover a parábola 2 unidades para a esquerda $ x^2 $ é alterado para $ (x + 2)^2 $ (parábola verde na Figura 5). Para mover a parábola 2 unidades para a direita $ x^2 $ é alterado para $ (x - 2)^2 $ (parábola azul na Figura 5). Outra propriedade que pode ser percebida é que todos os movimentos efetuados até o momento mudaram a posição do vértice da parábola. Portanto, apenas olhando para a equação $ y = (x + 2)^2 - 2 $ é possível dizer que o vértice da parábola está no ponto (-2, -2). Dessa forma, podemos mover a parábola pensando apenas onde deve ficar o vértice.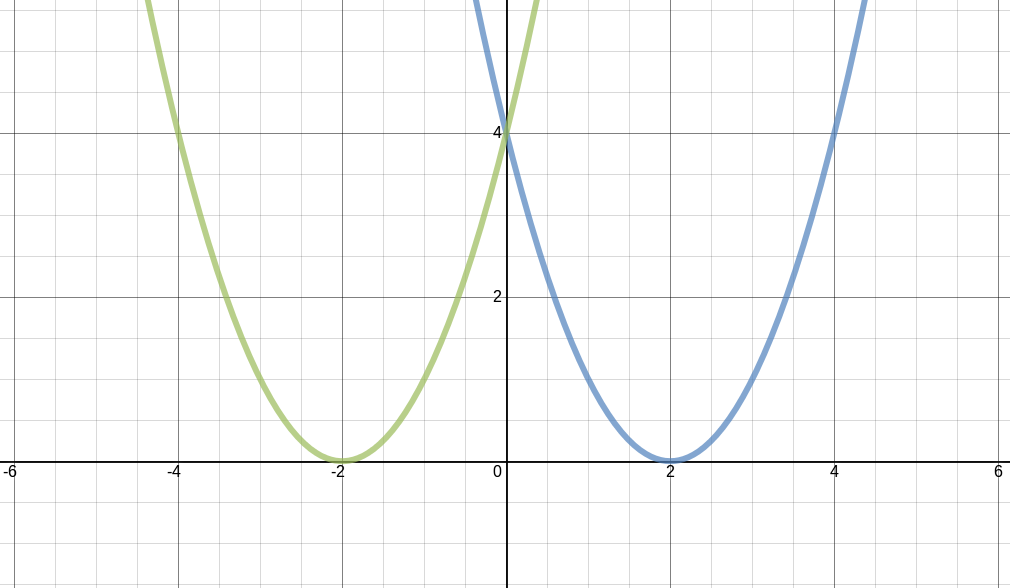
Figura 5 - Exemplos de transformações em parábolas no eixo x.
Além de movimentar a parábola, também é possível alterar a sua largura. Essa propriedade é controlada pelo coeficiente de $ x^2 $. Para que a parábola seja mais larga, deve-se diminuir o coeficiente de $ x^2 $. Por exemplo, $ y = \frac{1}{4}x^2 $ (parábola roxa na Figura 6) e $ y = \frac{1}{2}x^2 $ (parábola azul na Figura 6). Para que a parábola seja mais estreita, deve-se aumentar o coeficiente de $ x^2 $. Por exemplo, $ y = 2x^2 $ (parábola laranja na Figura 6) e $ y = 4x^2 $ (parábola preta na Figura 6).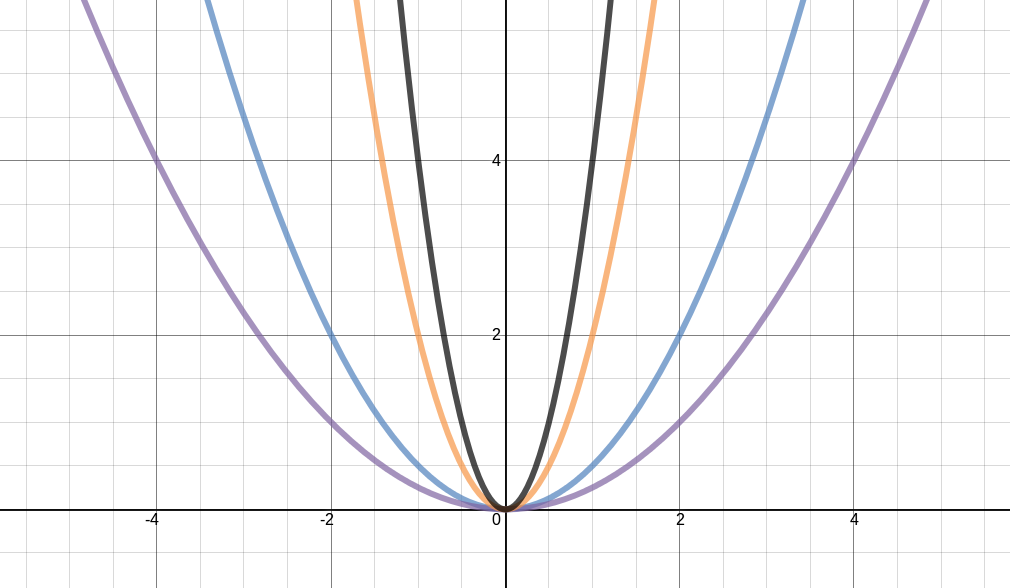
Figura 6 - Exemplos de transformações na largura da parábola.
Além da espessura da parábola, o coeficiente de $ x^2 $ também controla a direção da parábola. Com um coeficiente positivo ($ y = 5x^2 $), a parábola abre para cima (parábola vermelha na Figura 7) e com um coeficiente negativo ($ y = -5x^2 $) a parábola abre para baixo (parábola azul na Figura 7).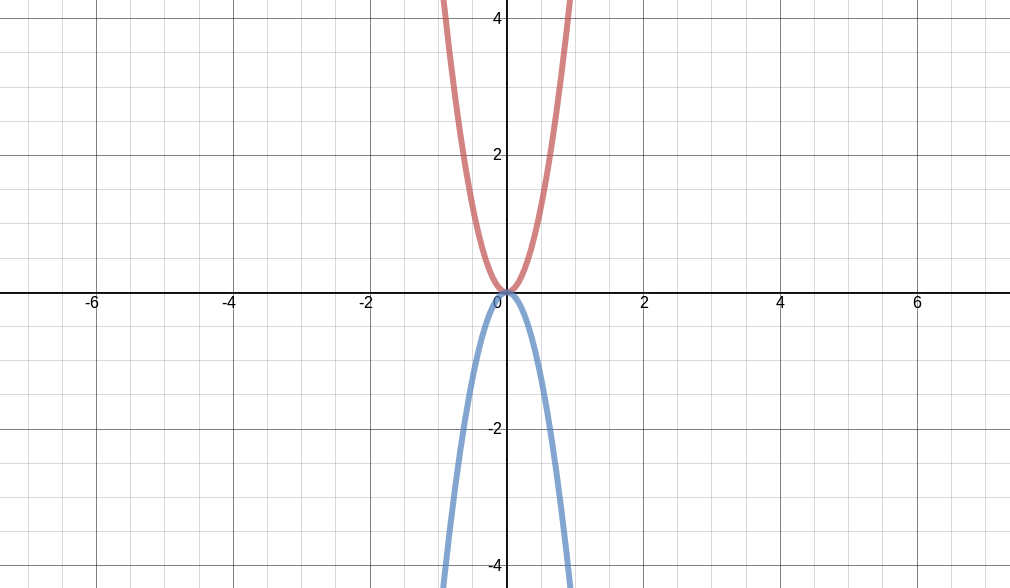
Figura 7 - Exemplos de transformações na direção da parábola.
Correndo atrás do próprio rabo: desenhando as laterais das asas com círculos
As laterais das asas podem ser desenhadas com dois meio círculos como pode ser visto na Figura 8.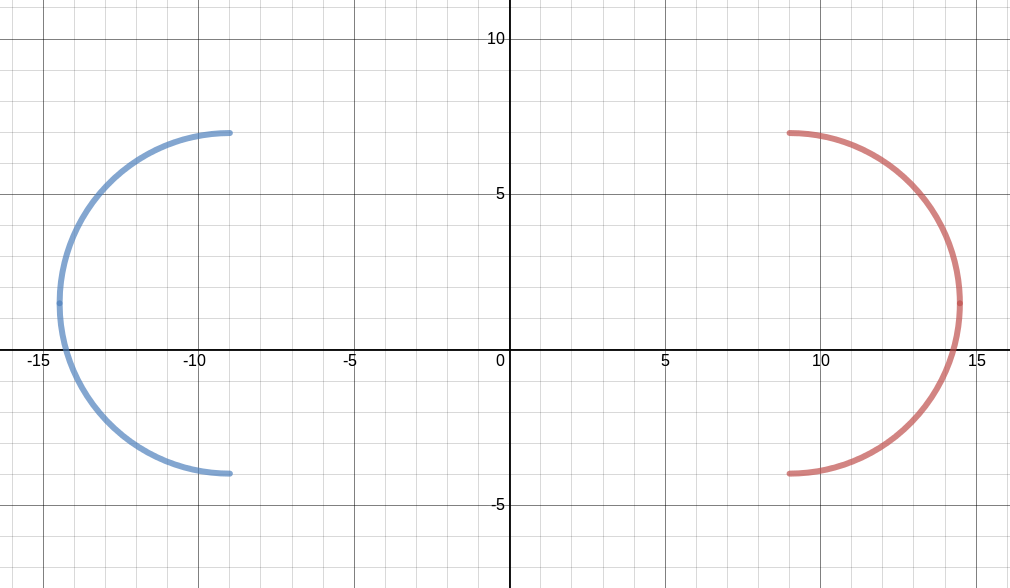
Figura 8 - Asas completas com círculos completando as laterais das asas.
Por que os círculos se comportam dessa forma?
A equação básica para um círculo é $ x^2 + y^2 = 4 $, sendo $ 4 = r^2 $. A partir dessa equação é possível explorar as mesmas propriedades que já vistas nas parábolas e retas. Para movimentar o círculo no eixo x, é preciso mudar a base de $ x^2 $. Por exemplo, a equação para movimentar o centro 2 unidades para a esquerda é $ (x + 2)^2 + y^2 = 4 $ (círculo verde na Figura 9) e a equação para movimentar 2 unidades para a direita é $ (x - 2)^2 + y^2 = 4 $ (círculo roxo na Figura 9). A mesma ideia vale para movimentar no eixo y. A equação para movimentar 2 unidades para cima é $ x^2 + (y - 2)^2 = 4 $ (círculo preto na Figura 9) e a equação para movimentar 2 unidades para baixo é $ x^2 + (y + 2)^2 = 4 $ (círculo laranja na Figura 9).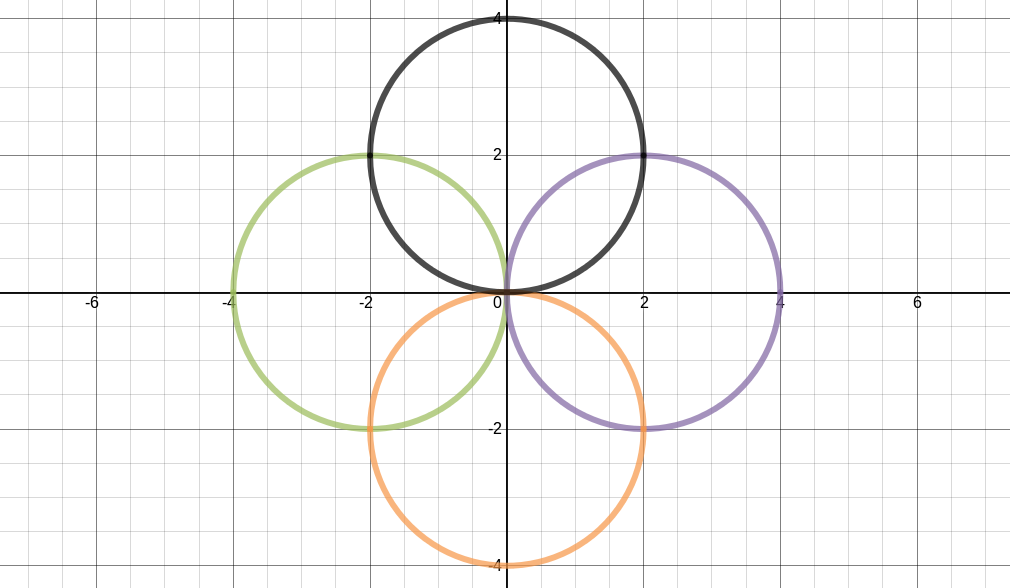
Figura 9 - Exemplos de transformações no círculo nos eixos x e y.
Também é possível controlar o tamanho do círculo. Para isso, é necessário alterar o termo do lado direito da equação ($ r^2 $). Por exemplo, a equação $ x^2 + y^2 = 9 $ (círculo azul na Figura 10) desenha um círculo maior que a equação $ x^2 + y^2 = 5 $ (círculo vermelho na Figura 10).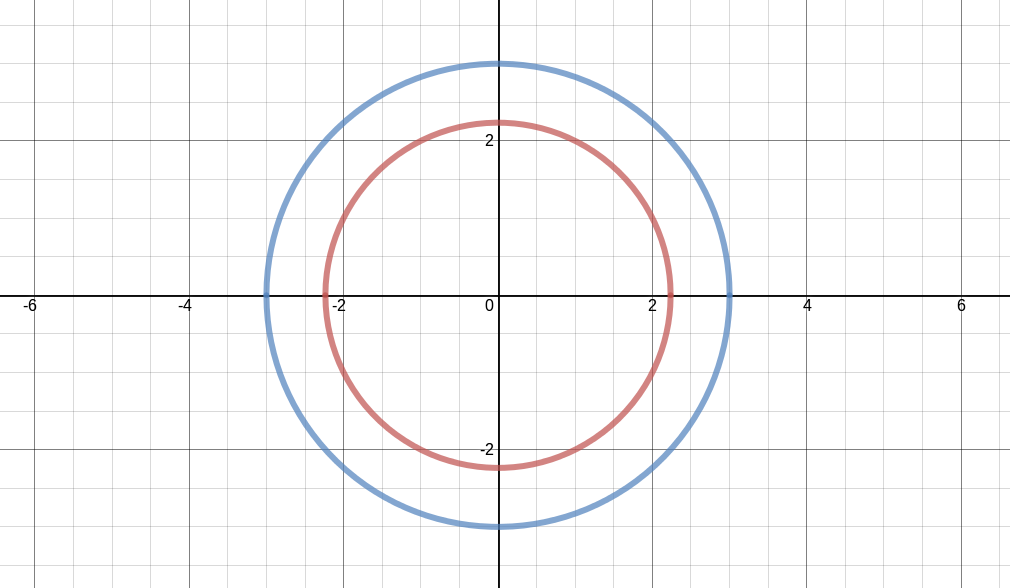
Figura 10 - Exemplos de transformações no tamanho do círculo.
É isso por hoje. Abraços e até a próxima :D.